Why and when the analogies in the word2vec algorithms work
Od publikování prvního algoritmu Tomáše Mikolova, převádějícího slova na vektory se zajímavými vlastnostmi (psal jsem o něm zde), uběhlo již několik let. Stále se však lidé snaží více či méně uspokojivě vysvětlit, jak je možné, že "kings – king + queen = queens". Před časem napsal podobný text na svém blogu Piotr Migdal. Článek je inspirativní, ale obsahuje řadu nepodložených tvrzení a předpokladů. Rád bych zde prezentoval alternativní zdůvodnění vycházející ze stejných myšlenek, které však bude preciznější.
Jedním z hlavním přínosů většiny takzvaných word embedding algoritmů (cbow, skipgram, glove, atd.) je schopnost projektovat lexikální jednotky (nejčastěji slova) do vektorového prostoru, ve kterém morfologické, syntaktické i některé sémantické vlastnosti těchto slov zachovávají lineární závislosti. Znamená to, že když například vektor slova king odečteme od vektoru slova kings, dostaneme vektor, který lze významově chápat jako vektor přechodu od singuláru k plurálu. Pokud tento vektor přičteme k libovolnému substantivu v singuláru, dostaneme se v daném vektorovém prostoru velmi blízko k vektoru stejného slova v plurálu. Tuto vlastnost ilustruje známý obrázek převzatý z původního článku T. Mikolova.
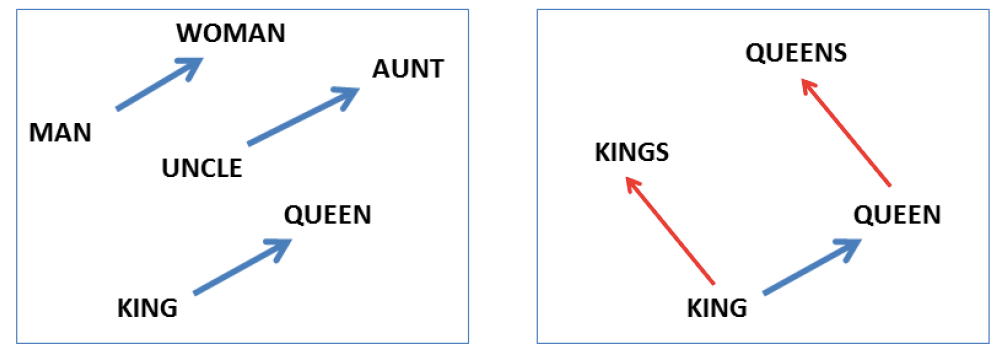
Obrázek 1: Vektorová reprezentace slov. Zdroj: T. Mikolovov et al. : Linguistic Regularities in Continuous Space Word Representations, NAACL 2013.
Tohoto fenoménu lze využít k hledání slovních analogií. Mohli bychom se ptát na slovo W, pro které platí: king se má ke kings jako queen k W. V obecnosti bychom chtěli ukázat, že pokud se slovo a má ke slovu A stejně jako slovo b ke slovu B, potom přibližně platí va – vA = vb – vB, kde vx je vektor reprezentující slovo x, získaný některým z algoritmů word2vec (viz Obr. 1).
Word2vec je zobecňující pojmenování pro metody převodu slova na jeho vektorovou reprezentaci. Pro účely tohoto textu se zaměřme konkrétně na nejznámější algoritmus Skip-gram s negativním samplováním.
Abychom mohli dané tvrzení dokázat, je třeba se nejdříve vypořádat s vágní definicí vztahu “mít se stejně k”. To většina literatury zanedbává a spokojuje se jen s intuicí. Pro větší přehlednost budeme v následujícím textu tučnou kurzívou označovat lexikální jednotky, kurzívou jejich vlastnosti a tučně zápis lexikální jednotky v korpusu.
Vyjděme z Firthova pohledu na lexikální význam. Jeho známý citát „You shall know a word by the company it keeps“ lze, volně přeloženo, chápat tak, že význam slova je dán slovy, která se s ním často pojí. Podle jeho tvrzení tedy platí, že dvě slova mají podobný význam tehdy, když se v textech často vyskytují ve stejných kontextech. Jedná se o v praxi často využívaný pohled na lexikální sémantiku.
Význam slova a lze ve Firthově pojetí formalizovat jako soubor pravděpodobností SEM(a) = 〈P(w | a): w ∈ L〉, které vyjadřují pravděpodobnost výskytu slova w blízko slova a v jazyce L. Ten nechť je reprezentovaný dostatečné velkým jazykovým korpusem. Blízkost je určena nějakou maximální vzdáleností v textu (měřeno počtem slov, která je oddělují).
Dalším důležitým poznatkem je Fregeho princip kompozicionality, který nám říká, že význam složitějšího lexikálního výrazu je dán významem dílčích jednotek a způsobem jejich kombinace. Tento princip se dá vztáhnout i na význam slov – slovo je nositelem souboru dílčích významů, která dohromady dávají význam celého slova. Například slovo queen lze zjednodušeně chápat jako anglické substantivum označující osobu, která má současně vlastnosti být panovníkem s královským titulem a být ženského pohlaví.
Vycházejíce z předchozích dvou formulací můžeme tedy význam slova queen definovat pomocí pravděpodobností〈P(wi | je panovník ∧ je ženského pohlaví )〉, v obecnosti jako 〈P(wi | a1, a2, … an)〉.
Nyní již lze zadefinovat slovní analogie: a se má k A stejně jako b k B tehdy, když existují vlastnosti a1... an, b1... bn, c a d takové, že
SEM(a) =〈P(wi | a1, a2, … an, c)〉
SEM(A) =〈P(wi | a1, a2, … an, d)〉
SEM(b) =〈P(wi | b1, b2, … bm, c)〉
SEM(B) =〈P(wi | b1, b2, … bm, d)〉.
Pokud budou platit následující statistické nezávislosti výskytů vlastností slov v korpusu
P(a1, a2, … an) ⊥ P(c)
P(a1, a2, … an) ⊥ P(d)
P(b1, b2, … bm) ⊥ P(c)
P(b1, b2, … bm) ⊥ P(d)
Dostaneme pro všechna wi
neboť
.
Nyní již lze analogie snadno zdůvodnit
Přičemž z definice pointwise mutual information platí
.
Teď využijeme výsledek práce Levy & Yoav Goldberg, 2014, kde bylo ukázáno, že algoritmus Skip-gram s negativním samplováním aproximuje rozklad matice slov a kontextů, kde jednotlivé buňky matice odpovídají (až na konstatní posuv) pointwise mutual information. Autoři Arora & kol., 2015 sice ukazují, že aproximace se blíží skutečnosti jen u vektorů vysoké dimenze a navrhují vlastní důkaz, pro potřeby tohoto článku nám však tvrzení stačí:
.
Odsud již dostaneme kýženou lineární závislost vektorů, odpovídající slovním analogiím:
.
Problémem důkazu je předpoklad nezávislosti výskytu jevů v korpusu, který samozřejmě ve většině případů neplatí. To je něco, čím se žádný ze mně známých důkazů analogií v algoritmech word2vec kvůli vágní nebo chybějící definici významu slov nezabýval. Je možné, že existuje silnější důkaz, který předpoklad nezávislosti jevů nepotřebuje. Druhou možností je, že slovní analogie fungují přesně jen v případě statisticky nezávislých jevů. Ani pro jedno však nemám zdůvodnění, a proto nechávám otázku otevřenou pro případné zájemce z řad čtenářů.
Pro tuto chvíli však nechme stranou exaktní důkazy a podívejme na několik příkladů analogií napočítaných algoritmem skip-gram na korpusu českého internetu.
| + slovo | - slovo | + slovo | nejbližší slovo výsledku | kosinová podobnost |
|---|---|---|---|---|
| královna | král | řidič | řidička | 0.785 |
| Řidička | 0.682 | |||
| cyklistka | 0.625 | |||
| rybářka | rybář | ošetřovatel | ošetřovatelka | 0.692 |
| Ošetřovatelka | 0.619 | |||
| canisterapeutka | 0.605 | |||
| královna | kozel | řidič | řidička | 0.609 |
| čtyřiadvacetiletá | 0.532 | |||
| dvaadvacetiletá | 0.511 | |||
| rybářka | kozel | ošetřovatel | krotitelka | 0.574 |
| ošetřovatelka | 0.547 | |||
| pasačka | 0.541 |
V tabulce jsou vždy uvedena tři slova, která slouží jako dotaz a ke každému dotazu 3 nejbližší slova nalezená v prostoru spolu s kosinovou podobností. U prvního příkladu, kde je dotazem v(královna) – v(král) + v(řidič) vidíme, že analogie krásně fungují a dvě nejbližší nalezená slova jsou řidička a Řidička. Ve druhém příkladu byla záměrně použita slova, pro která předpoklad nezávislosti výrazněji neplatí. Vlastnost být rybářem a být muž, spolu jistě pozitivně korelují. Podobně jako vlastnosti být ošetřovatel a být žena. Přestože kosinová podobnost nejbližšího kandidáta je nižší než v předchozím případě, stále je výsledkem správná odpověď ošetřovatelka. Třetí příklad je extrémnější. Dotazem je zde v(královna) – v(kozel) + v(řidič) a výsledkem stále řidička, i když už s výrazně nižší kosinovou podobností. Tento výsledek je trochu zarážející a neodpovídá naší intuici. Zdá se, že vlastnost být mužem a být ženou je natolik dominantní, že převáží všechny ostatní. Teprve poslední příklad, který kombinuje extrémy předchozích ukázek, dopadne jinak. Na dotaz v(rybářka) – v(kozel) + v(ošetřovatel) najdeme jako nejbližší slovo krotitelka.
Těchto pár příkladů samozřejmě vůbec nic nedokazuje. Je z nich však vidět, že hledání analogií pomocí word2vec přístupů je velmi odolné vůči šumu. Může tedy dobře fungovat i v případě, že by byl pro přesný důkaz požadavek nezávislosti jevů nutný. Navíc nepřesností, které do procesu hledání analogií vstupují, je mnoho (velikost a zaměření korpusu, velikost reprezentujících vektorů, apod.) a je jen otázkou, jak velkou chybu jednotlivě způsobují. Velká odolnost vůči nim je podle mého názoru zajištěna velkou řídkostí vektorového prostoru, ve kterém analogie hledáme. Pro dotaz v(královna) – v(kozel) + v(řidič) najdeme jako odpověď slovo řidička jednoduše proto, že se v blízkosti žádné jiné slovo nenachází.
Convergence of the k-means algorithm
U pohovorů na pozici výzkumníka v Seznamu se ptávám na principy vybraných algoritmů strojového učení, mezi které patří i k-means pro shlukování. Po tom, co algoritmus dáme dohromady, následuje otázka, zda je zaručené, že algoritmus vždy skončí. Tušil jsem, že se dají najít extrémní případy, kdy algoritmus může začít nekonečně dlouho kmitat mezi několika stejně dobrými řešeními, a tak jsem požadoval drobné doplnění ukončovací podmínky (například detekci cyklu), která by ukončení garantovala.
Nedávno jsem však narazil na uchazeče, který byl skálopevně přesvědčený, že standardně definovaný k-means skončí za všech okolností a přísnější kritérium není potřeba. Vzhledem k tomu, že jsem žádný protipříklad připravený neměl, zkusil jsem nejprve zahledat na internetu. A ejhle. Internet je plný „důkazů“ toho, že k-means konverguje. Tvrdí to dokonce i Wikipedie! Nezbylo mi tedy nic jiného, než ten protipříklad vymyslet. Tady je.
Algoritmus k-means
K-means patří do skupiny takzvaných algoritmů strojového učení bez učitele. Jeho cílem je nalezení k shluků daných bodů, kde shlukem rozumíme skupinu bodů, které jsou si navzájem blízko (ve smyslu nějaké metriky). Typickým příkladem použití může být analýza zákazníků internetového obchodu, které chceme podle zájmů a chování roztřídit do předem neznámých kategorií.
Vstupem algoritmu je množina m bodů, které jsou definované souřadnicemi v n-rozměrném prostoru, a číslo k, určující požadovaný počet shluků. Všechny shluky jsou reprezentované svými středy a každý bod potom náleží do shluku, jehož střed je mu nejblíže. Souřadnice středů se určují iterativním způsobem založeným na EM algoritmu. Zde uvádím jeho neformální zápis (zájemci o preciznější definici si ho můžou nastudovat na příklad na Wikipedii):
- Pro každý shluk zvol náhodně souřadnice jeho středu (typicky se volí totožně se souřadnicemi náhodně vybraných různých bodů).
- Každý bod přiřaď středu, ke kterému leží nejblíže.
- Urči nové souřadnice středů jako průměr souřadnic všech bodů, které náleží do daného shluku.
- Opakuj od bodu 2, dokud se shlukování neustálí.
Princip algoritmu je ilustrovaný obrázkem 1.
Není obtížné dokázat, že tento iterativní algoritmus neustále zmenšuje chybu, definovanou jako součet vzdáleností všech bodů od středů svých shluků, a spěje tak k nějakému lokálně-optimálnímu řešení. Co však, pokud dojde k tomu, že má jeden bod stejně daleko ke středům dvou nebo více různých shluků? V takovém případě je možné náhodně vybrat libovolný z nich a v tom je kámen úrazu.
Protipříklady
Začněme velmi jednoduchým příkladem. Mějme pouze dva body, které leží přesně na sobě, a hledejme 2 shluky. Pokud budou jejich středy inicializovány do stejného místa jako shlukované body, máme problém, neboť v kroku 2 algoritmu bude mít každý bod stejně daleko ke dvěma středům, a může si tak vybrat odlišný od toho z předchozí iterace. Tím se změní shlukování a algoritmus tak pokračuje dál. Takto je možné kmitat mezi čtyřmi řešeními libovolně dlouho a algoritmus nemusí nikdy skončit.
Dalo by se namítnout, že se v tomto jednoduchém příkladu oba shluky překrývají a nemuseli bychom je tedy považovat za různá řešení. Lze však vymyslet i netriviální příklady.
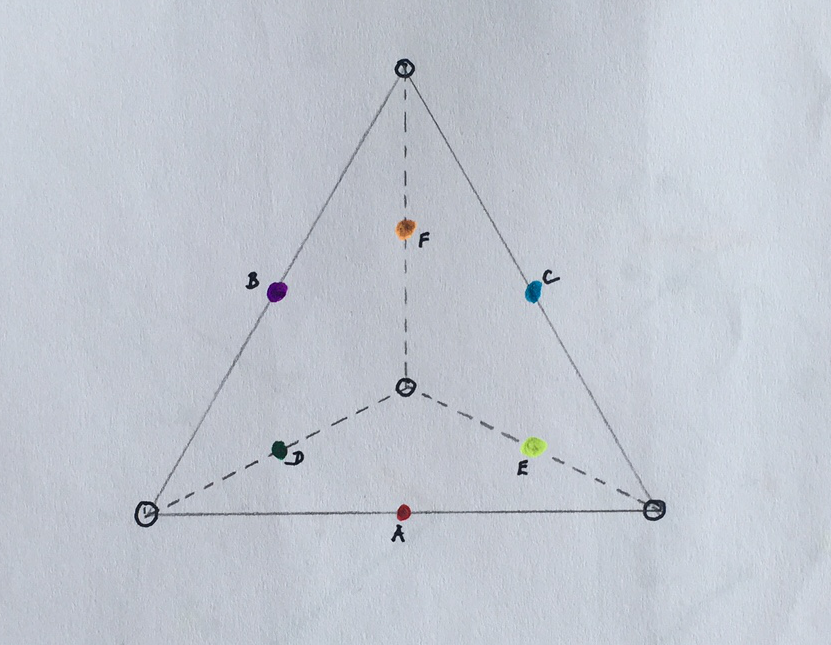
Mějme 10 bodů v trojrozměrném prostoru, které leží na vrcholech a v polovinách středů hran pomyslného pravidelného čtyřstěnu, a hledejme 6 shluků, jejichž středy A, B, C, D, E, F jsou inicializovány do středů hran, jak je ilustrováno na obrázku 2.
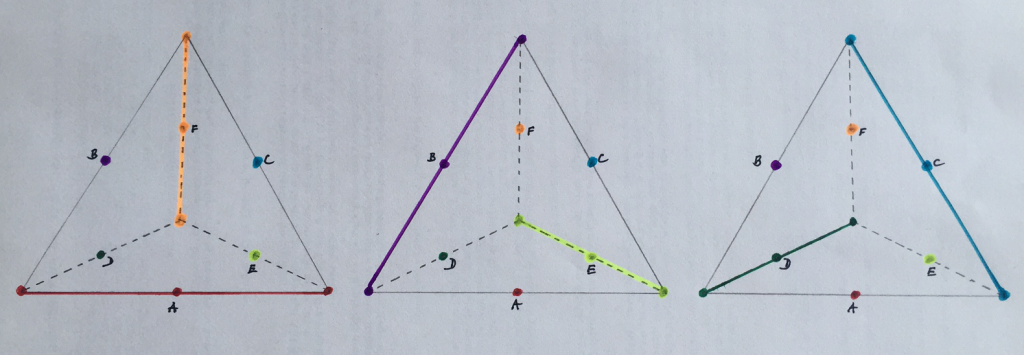
V takovém případě jsou vždy body na vrcholech stejně daleko od tří různých středů a je možné je tedy přiřadit třem různým shlukům. Existují tři různá shlukování, mezi kterými může algoritmus kmitat, aniž by zkonvergoval. Tato různá řešení jsou znázorněna na obrázku 3.
Klasický algoritmus k-means tedy v extrémních případech konvergovat nemusí. Opatření, která jeho skončení zajistí jsou však snadná. Nejjednodušším z nich je determinizace výběru shluku v případě, že máme více možností. Shluky si můžeme očíslovat a místo náhodného výběru vybírat například vždy ten s nejnižším identifikátorem. Jinou možností je detekovat kmitání nebo změnit ukončovací podmínku algoritmu a zastavit v případě, že už se chyba shlukování nezmenšuje. Nic takového však standardní definice algoritmu neuvádějí a tvrzení, že k-means vždy konverguje je tedy nesprávné.
Is singularity near?
Dnes proběhlo poslední kolo mediálně ostře sledovaného poměřování schopností člověka a stroje. Počítačový program AlphaGo firmy DeepMind ve hře Go definitivně potvrdil své vítězství a porazil tak dosavadního mistra světa Lee Sedola s výsledným skóre 4:1. Go se od šachu nebo jiných her, ve kterých stroje porazily člověka už dávno, liší v obrovské velikosti prostoru herních možností. Tento prostor není možné procházet celý a hledat globálně optimální tah, namísto toho je potřeba využít jakési strojové intuice, která vychází pouze z lokálních znalostí. Intuice, kterou jsme doposud přisuzovali pouze lidem, se v souvislosti s AlphaGo v popularizačních textech zmiňuje poměrně často. Může se tedy zdát, že se přiblížila doba, kdy nás počítače svojí inteligencí překonají.
Vítězství stroje nad šampiónem v Go je bezpochyby významný úspěch vývojářů DeepMind, ale je singularita skutečně blízko? Nemyslím si.
Singularita
Pojem singularita v kontextu umělé inteligence zavedl matematik Stanislaw Ulam v polovině dvacátého století. Jedná se o hypotetickou událost, kdy univerzální umělá inteligence dosáhne úrovně člověka a svojí schopností vylepšovat sebe sama nás začne rychle překonávat. Nemalé množství lidí věří, že se tato chvíle velice rychle blíží.
Jedním z nejznámějších popularizátorů singularity je Ray Kurzweil, který se proslavil především jako autor knihy The Singularity Is Near: When Humans Transcend Biology. Hlavním argumentem pro blížící se singularitu je dosavadní exponenciální růst různých forem technologického pokroku. Tato myšlenka je rozšířením takzvaného Moorova zákona, podle kterého se počet tranzistorů umístěných na počítačový čip zdvojnásobuje zhruba každé dva roky. Jedním z příkladů rozšíření je exponenciální růst výpočetní rychlosti počítačů, ilustrovaný na obrázku 1.
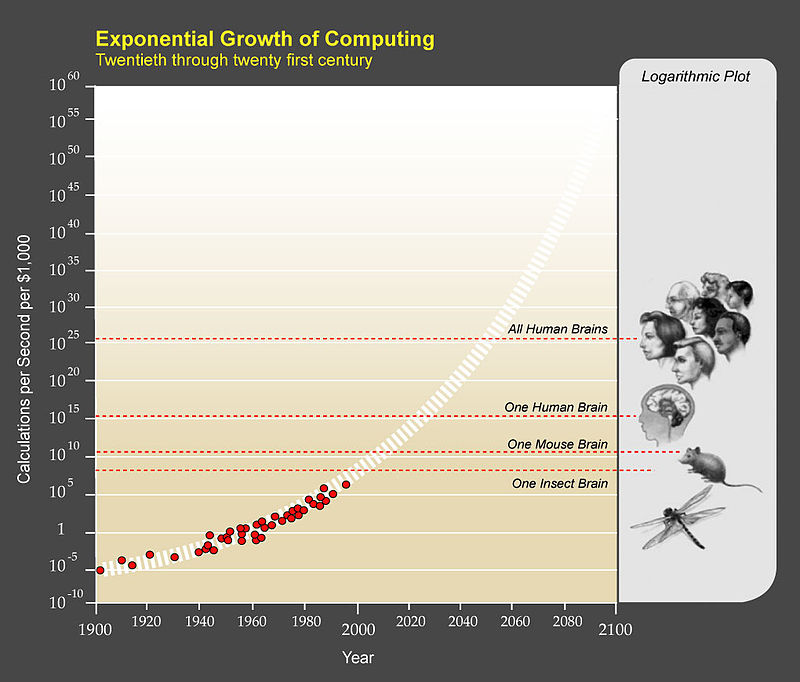
Obrázek 1: Exponenciální růst výpočetní rychlosti. Zdroj: https://en.wikipedia.org/wiki/The_Singularity_Is_Near
Je ale exponenciální růst výpočetní rychlosti a dalších technologických ukazatelů dostatečným předpokladem k dosažení umělé inteligence, překonávající ve všech ohledech intelekt člověka?
Úspěchy umělých neuronových sítí
Není pochyb o tom, že existuje celá řada oblastí, ve kterých stroje nad lidmi výrazně vynikají. Už od dob prvních počítacích strojů to jsou úlohy, vyžadující mechanické opakování rutinních postupů. V posledních letech však slaví stroje úspěchy i v oblastech, které byly doposud pouze doménou člověka. Jmenujme například rozpoznání obsahu obrázku, kde současný nejlepší algoritmus dosahuje chybovosti 4,58 % (chybovost člověka se údajně pohybuje někde kolem 5 %), algoritmy pro řízení aut a dronů, projekt DeepDream firmy Google, vytvářející psychedelické obrazy, v úvodu zmíněný program AlphaGo, nebo třeba systém, který je schopný psát básně.
Všechny tyto úlohy mají dvě společné vlastnosti. První z nich je vysoká dimenzionalita problému – u algoritmů pro zpracování obrazu je to množství vstupních pixelů, které nedávají velký smysl jednotlivě, ale je třeba se na ně dívat jako na celek, u hry Go je to obrovské množství možných herních scénářů, u generování textů souvisí vysoká dimenzionalita s množstvím různých kombinací slov, které mohou mít pokaždé úplně jiný význam. Druhým jednotícím prvkem je fakt, že současných fascinujících výsledků bylo dosaženo pomocí hlubokých neuronových sítí.
Umělé neuronové sítě však známe již několik desítek let, je tedy legitimní pokládat otázku, co náhlý posun umožnilo. V první řadě je důležité si uvědomit, že se zmíněné úlohy v principu neliší od jiných úloh strojového učení, které už dlouhé roky považujeme za uspokojivě vyřešené. Nikdo se dnes nepozastavuje nad tím, že e-mailový server dokáže s velkou úspěšností správně rozpoznat spam, nebo nad tím, že cílená reklama na internetu velice přesně reflektuje nikde explicitně nespecifikované zájmy uživatele. Rozpoznávač obrázků není nic složitějšího než klasifikátor s komplexní vnitřní strukturou. Strojový generátor básní je svým způsobem také klasifikátor, jenž se na základě předchozího textu snaží predikovat jeho nejpravděpodobnější pokračování.
Systémy řízení dronů nebo algoritmus AlphaGo se od předchozích příkladů liší v tom, že v sobě zahrnují zpětnou vazbu od okolního prostředí, na základě které jsou schopny se dále zlepšovat. Pokud dron provede nějakou akci, kvůli které začne neočekávaně ztrácet výšku, je to pro něj jednoznačná zpráva o provedení chybného manévru, ze které se může poučit. Podobně algoritmus AlphaGo sehrál několik milionů her sám proti sobě, díky čemuž se dokázal naučit lépe odlišovat dobré strategie od horších. Tomuto způsobu učení se říká reinforcement learning a zdaleka nejde o žádný nový vynález natož o něco principiálně odlišného od neuronových sítí s jinou formou zpětné vazby.
Když opomeneme několik inženýrských triků urychlujících trénování, úspěch hlubokých neuronovým sítí v poslední době je způsoben pouze obrovským nárůstem výpočetního výkonu, který sítím v rozumném čase umožňuje vytvářet velmi složité vnitřní struktury a efektivně pracovat s daty vysoké dimenzionality. To však samo o sobě není všespásné.
Budoucnost umělé inteligence
V tuto chvíli umíme strojově efektivně řešit některé jednotlivé problémy, které se na první pohled zdají být složité, ale principálně příliš obtížné nejsou. Pokud bychom chtěli, aby se stroje vyrovnaly lidem ve všem, potřebovali bychom něco víc než jen výpočetní výkon. Pro ilustraci uvedu dva příklady, které přesahují rámec schopností známých algoritmů.
Současná umělá inteligence umí řešit pouze problémy, pro které je vytvořená. Stále je to jen algoritmus, vykonávající postupy naprogramované člověkem, a příliš se tak neliší třeba od výrobní linky v továrně. Oproti tomu člověk je schopný vidět svět v souvislostech a být kreativní. Pokud člověk vytvoří program, který umožňuje generovat básně, přirozeně ho napadne, že by se podobný algoritmus dal použít i pro generování notového zápisu hudby. Stroj ale tuto souvislost nevidí. Když učitel na základní škole přehraje dětem úryvek Smetanovy Vltavy a Blaníku, věřím, že většina žáků dokáže rozpoznat, který úryvek odkazuje k řece a který k rytířům, aniž by nad tím žáci kdykoliv přemýšleli nebo jim někdo řekl, podle jakého klíče se mají rozhodnou.
Jiným příkladem omezenosti stroje je absence jeho vlastního vědomí. Stroje se nerozhodují podle svého vlastního úsudku, ale buď podle pravidel, která jsou získaná z dat (případně jsou přímo součástí jejich algoritmu), nebo statisticky podle napočítaných pravděpodobností. Algoritmus pak sice dokáže provést správné rozhodnutí, ale je velice obtížné zjistit, proč se tak rozhodl. Natož, aby své rozhodnutí dokázal sám zdůvodnit. Při generování básní nemá počítač ponětí o tom, co vytváří, pouze aplikuje obecné vzory získané z dat a vytváří statisticky očekávané posloupnosti písmen.
Na základě svých znalostí a zkušeností si netroufám predikovat, zda se jednou podaří vytvořit univerzální umělou inteligenci, která se ve všem vyrovná člověku a postupně ho překoná. Jsem však přesvědčený, že k tomu teď nejsme o mnoho blíže než v polovině minulého století, kdy Alan Turing vytvořil první teoretický model výpočetního stroje.
The medieval age of artificial intelligence is over: meet a neural network that can write poetry
Nikdy jsem si nemyslel, že by jednou počítače mohly nahradit v člověka v tak kreativních a neexaktních činnostech jako je malba nebo skládání básní. Pomalu ale začínám měnit názor.
Není tomu dlouho, co se i v neodborných časopisech začalo psát o neuronových sítích, které dokáží generovat obrazy, připomínající psychedelické výtvory surrealistických malířů. Jak je to ale s automatickým generováním textů? Několik článků na toto téma vzniklo (např. http://karpathy.github.io/2015/05/21/rnn-effectiveness/), ale žádný zatím nezískal takový ohlas jako generátory obrazů. Pojďme tedy tuto oblast podpořit a ukažme si, jak pomocí umělých neuronových sítí vytvořit automatického básníka.
Rekurentní neuronové sítě
Většina neuronových sítí, které jsou používány k analýze i ke generování obrazu, je dopředných. To znamená, že signál v neuronové síti může proudit pouze jedním směrem a nemůže se vracet nebo se např. točit ve smyčce. Sítě, které toto umožňují se nazývají rekurentní. Takové sítě mnohem blíže připomínají lidský mozek a především mají jednu zásadní vlastnost — a tou je možnost uchování informace. Jinými slovy, rekurentní sítě mají paměť. Díky tomu je vyjadřovací schopnost těchto sítí větší než u dopředných neuronových sítí, a je dokonce dokázáno, že je ekvivalentní Turingovu stroji.
Paměť není nutná vždy, pokud však chceme pracovat se sekvenčními daty jako jsou texty, bez paměti se obejdeme jen stěží. Nevýhodou rekurentních neuronových sítí je však obtížnost trénování. Zatím existuje jen několik málo architektur rekurentních sítí, které dokážeme trénovat efektivně. Jednou z nich je takzvaná Long Short-Term Memory (LSTM), kterou použijeme jako stavební prvek našeho automatického básníka.
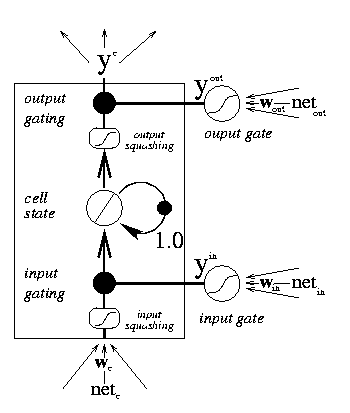
Jedna paměťová buňka Long Short-Term Memory je znázorněna na obrázku 1, převzatém z http://www.willamette.edu/~gorr/classes/cs449/lstm.html.
Její jádro tvoří stavový neuron spolu se zpětnovazební smyčkou, označený jako „cell state“. Díky zpětné vazbě je neuron schopný uchovávat informaci, která byla přivedena na vstup i poté, co je vstup odpojen. Připojení a odpojení vstupu je ovládáno neuronem označeným jako „input gate“. Podobně je aktivace výstupu řízena neuronem označeným jako „output gate“.
Automatický básník
Abychom mohli natrénovat neuronovou síť generující básně, potřebujeme jí ukázat, jak takové básně mají vypadat. K tomu by ideálně posloužil velký korpus básní. Vzhledem k tomu, že jsem žádný velký neměl k dispozici, použil jsem databázi písňových textů ze serveru supermusic.sk. Sice nejde o básně, ale písňové texy mají k poezii blízko. Pomocí jednoduché detekce jazyka byly odstraněny nečeské texy a vznikl tak 10 MB velký textový korpus. Kvůli oddělení jednotlivých písní byly jejich názvy ve formě nadpisů převedeny na kapitálky a samotné texty na malá písmena.
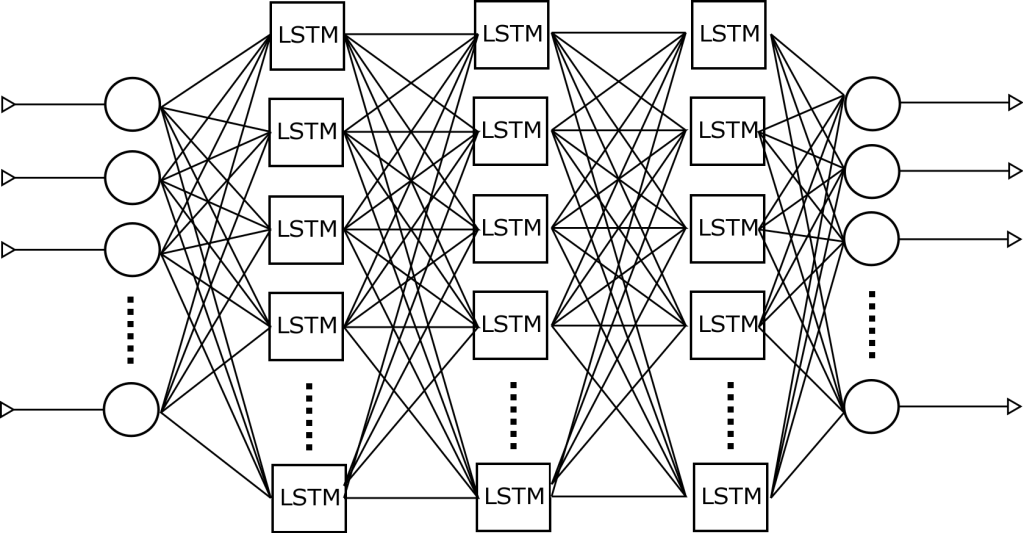
Neuronová síť pro generování básní je sestavena z pěti vrstev. Vstupní vrstva sestává ze 157 neuronů (což je počet různých znaků v korpusu). Následují tři vzájemně úplně propojené vrstvy LSTM, přičemž každou vrstvu tvoří 1024 buněk. Výstup je tvořen 157neuronovou softmax vrstvou, jejíž výstupem je pravděpodobnostní rozdělení přes 157 stavů. Architektura celé sítě je znázorněna na obrázku 2.
Síť je trénována tak, aby na základě historie a písmene na aktuální pozici v korpusu predikovala následující písmeno. Díky tomu, že síť pracuje na úrovni písmen a ne slov, jak by se nabízelo, je možné se naučit i formátování, specifické pro zápis písňových textů.
Vzrůstající popularita neuronových sítí s sebou přinesla celou řadu hotových nástrojů a knihoven. Není tak už naštěstí potřeba programovat vše od píky. Pro natrénování výše popsané sítě byla použita implementace Char-rnn využívající framework Torch.
Výsledek není vůbec špatný
Poté, co byla síť natrénovaná na písňovém korpusu, bylo možné ji použít pro generování nových textů. Pro účely testování byla inicializována náhodně, ale je možné ji inicializovat například i vložením názvu básně nebo počátečních veršů. Teoreticky může natrénovaná sít vygenerovat neomezené množství různých textů, nechal jsem tedy vygenerovat několik desítek básní a vybral pár nejlepších. Básně jsou přesně v té podobě, v jaké je vygenerovala síť.
Zde je jedna z nejlepších:
PÍSEŇ PODZIMU
proč se nedorazíš?
telefonát není naděje
pořád doma na týhle planetě
čas pro tebe stále dupe svouna na na...
já vím, že v duchu prozrazuju snář
poznám že nejsem nic víc
Soudě podle tohoto příkladu dokázala síť bezchybně použít českou slovní zásobu, morfologii i syntax. Nejzajímavější ale je, že i obsahově dává báseň víceméně smysl a není úplně hloupá. Dalo by se namítnou, že mohlo dojít k přetrénování a síť jen opakuje verše, které viděla při trénování. Pokud se však podíváme do korpusu, žádný z použitých veršů se tam nevyskytuje.
Je zřejmé, že je tato neuronová síť schopná pochopit i netriviální sémantické konstrukce. Příkladem může být přirovnání „vzácný jako listí“ v následující básni. Opět se jedná o sousloví, které se v korpusu vůbec nevyskytlo:
VŠE PRÝ JE MŮJ HŘÍCH
já nechci slyšet chtíč
tak vzácný jako listí
slzy v očích mám
a měl bych řvátkdo mi to vášně ukrývá
netuším, každý je tu sám
jen pár let jsem přísahal
že pro mne má smysl žít.
Obecně se dá říci, že čím kratší báseň je, tím větší smysl dává. Je to samozřejmě dáno tím, že v delších textech je větší prostor pro odbočení od tématu. Občas má síť tendenci vytvořit velmi krátkou báseň. Pokud to udělá, téměř vždy se jedná o něco povedeného a úsměvného. Zde jsou dva příklady:
NEJSI TAMARA
jsi ludmila
NEJHEZČÍ DÁREK
50 kčs, tak mám tě rád
Někdy se stane, že si síť vymyslí nové slovo. Pokud k tomu dojde, často se však jedná o velmi zajímavý novotvar jako v názvu následující básně:
DŽÍNOVÁ POKROPANÍ
tak přestaň, smiř se s tím
moje řeč, můj dech, být svá bez peněz
myslím, že jsi žena co dech ti dá
s tebou už nevím co s tímkdyž večer temně září
chuť ve mně zůstane
jen v klidu mi tvý kroky jdou
už dávno se smějezkouším se vrátit
nechci se ptát
hledám skrýš
každou noca pak se ztratí
neumím lhát
a nejde to vrátit
A na závěr několik dalších výtvorů různých kvalit:
NEJSI
sníh a mrazivá
vím vímproč zrovna jedna z tebe chce žít
to není možný ty to víš
a já mám ho rád
jen tak promlouvejztrácím sílu žít
PROČ SE MI ZDÁ
já vím, že jsem sám
a tak to mám rád
a tak se mi zdá
že tě nechci bítjá vím, že tě nechci bít
já vím, že jsem jen tvůj
ZÁTONÍ
nikdo nemá kolotoč.
krásné paže hostí,
troubí žlutejch koní
a k večeru opilí.déšť očima život hledá,
musím odeslat je dál,
protože jsi laciná
přece dobře už není.člověk náš kruh co pustý sen
chceš-li vedle nosit chlast.
oh, jak miliady třeští?
pak mi řekli: nebudeš, tak se střež
KRÁLOVNA VČEL
nebude to divně znít,
pozor na tvůj strach
nesměj se hned
a hned od lidíproč pocit mi nedáš,
nechci to hned
chceš mi říkat zatím starý poslání
když to ale nevíš, nevadíposlední ráj,
hledám nahoru a dolů
že je nevěrná
ať není dálvenku je den
tak proč se bojíme
spátdobře víme
že je něco v ní
a já už to vímooou jé
Pokud vás zajímají další příklady počítačem generovaných básní, můžete si zdarma stáhnout mou básnickou sbírku Poezie umělého světa. Pro vygenerování obsažených básní byl použitý vylepšený algortitmus napsaný v TensorFlow a jako trénovací sada posloužily básně ze serveru Písmák.cz.